data structures & algos

Big O & Recursion

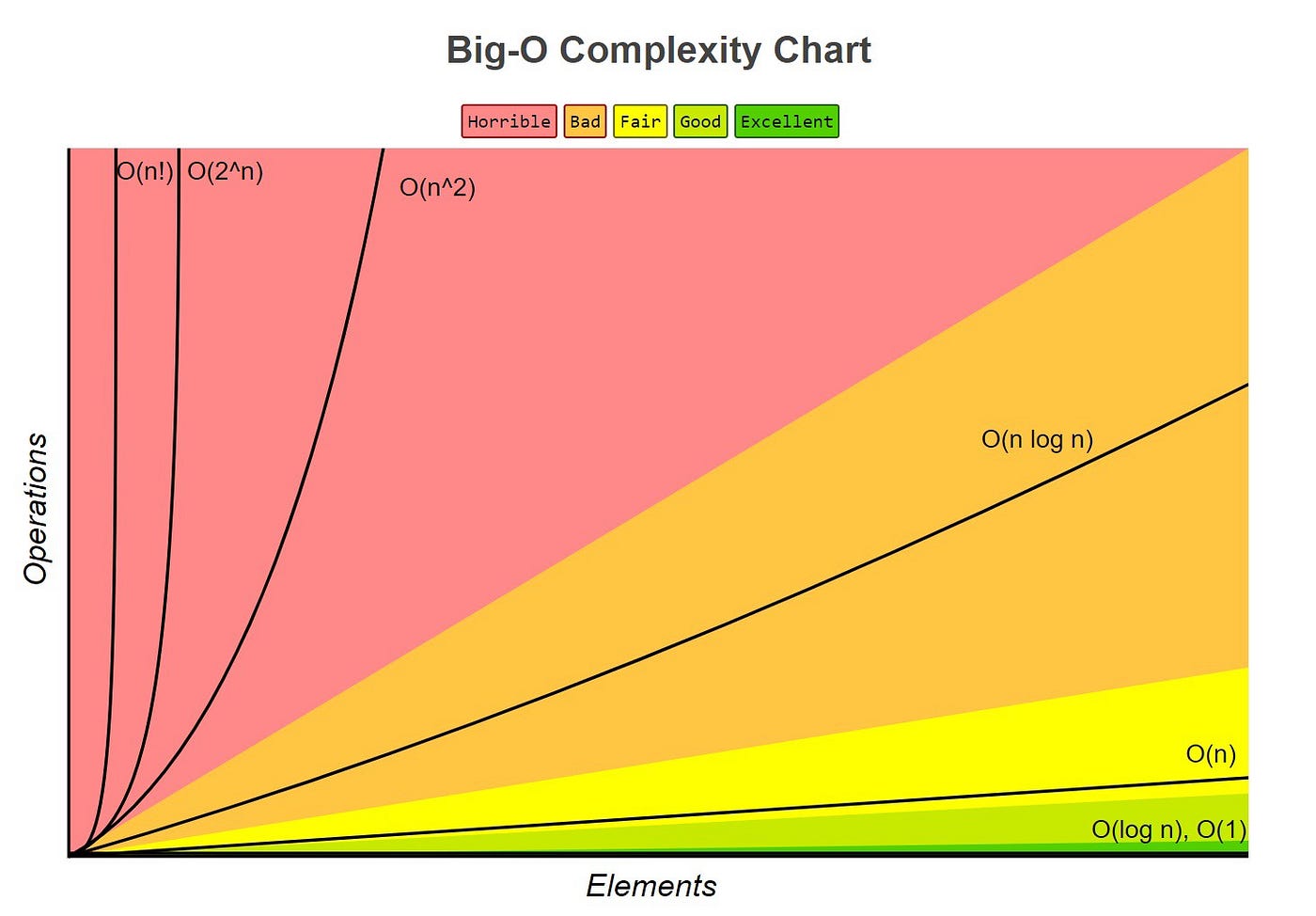
Intuition of O(log(n))

Log time $O(log$ $n)$: Means that somewhere in algo, input is reduced by a percentage at each step (i.e., binary search where step 1 is n/2 and step 2 is n/4, etc.)

Recall that $\log_b a = x$ and $b^x = a$
Say we have an array with length $n = 8$ so $\log_2 8 = 3$ and $2^3 = 8$
Because $x = 3$, we now only need to halve our 8 element array 3 times to find an element
Instead of iterating through all the elements with complexity $O(n)$, we do it in $O(log$ $n)$

Recursion:

def f(n):
    print(f(n+1))

This function would never stop running
We need a BASE CASE which specifies when the recursion ends

Base cases are specified at the start of the function

def fn(i):
    if i > 10:
        return
    print(i)
    fn(i + 1)

Example

def tri_recursion(k):
  if(k > 0):
    result = k + tri_recursion(k - 1)
    print(result)
  else:
    result = 0
  return result

print("\n\nRecursion Example Results")
tri_recursion(6)

Initial Call: tri_recursion(6)

k is 6, which is greater than 0.
It calls tri_recursion(5)
which calls tri_recursion(4)
All the way to tri_recursion(1)
Which calls tri_recursion(0) hitting the base case, and = returns 0.

Returning Back Up the Stack

Returning to tri_recursion(1)
The result of tri_recursion(0) is 0.
It calculates and returns result = 1 + 0 = 1.
Returning to tri_recursion(2) which calculates result = 2 + 1 = 3.
Returning to tri_recursion(3) which calculates result = 3 + 3 = 6.
All the way to returning to tri_recursion(6), where result of tri_recursion(5) is 15.
It calculates result = 6 + 15 = 21

1. Array and Strings

Rows & Columns

Transpose matrix

Iterate through number of row
- Iterate through number of columns
- switch rows and columns so matrix[columns][rows]

numRows = len(matrix)
numCols = len(matrix[0])
transposed = []
for row in range(numRows):
    newCol = []
    for col in range(numCols):
        newCol.append(matrix[col][row])
    transposed.append(newCol)

Print the next index:

arr = [0,1,2,3,4]
for i in range(len(arr) - 1):
    print(arr[i], arr[i+1])

Two Pointers

***Algorithm

Start with two pointers left and right
Iterate these two pointers along an array or string index
*Usually start code with while left < right

Ex: Check if string is palindrome:

def palindrome(n):
    left = 0
    right = len(n) - 1
    
    while left < right:
        if n[left] != n[right]:
            return False
        else:
            left += 1
            right -= 1
    
    return True

Ex: Check if there exists a target = sum of two numbers, in sorted array:

Start summing left and right
Because array is sorted, we can just move right pointer left if sum is too big, and left pointer right if too small

def sorted_twosum(array, target):
    left = 0
    right = len(array) - 1
    
    while left < right: 
        current = array[left] + array[right]
        if current == target:
            return True
        elif current < target:
            left += 1
        elif current > target:
            right -= 1
    
    return False

Using two pointers to iterate through two arrays:

Start both pointers at the first index
Use while loop until one pointer reaches end
At each iteration of the loop, move one or both of the pointers forward

Ex: Merge two sorted arrays:

def merge(arr1, arr2):
    ans = []
    i = j = 0
    while i < len(arr1) and j < len(arr2):
        if arr1[i] < arr2[j]:
            ans.append(arr1[i])
            i += 1
        else:
            ans.append(arr2[j])
            j += 1
    
    # finish iterating through the remainder array
    # only one of these blocks will be executed 
    while i < len(arr1):
        ans.append(arr1[i])
        i += 1
    
    while j < len(arr2):
        ans.append(arr2[j])
        j += 1
    
    return ans

Ex: Check if string A is a subsequence of string B:

Init two pointers for string A and B
If pointers match, move both pointers to the next letter
If no match, move pointer for String B to next letter

def subseq(a,b):
    i = j = 0
    while i < len(a) and j < len(b):
        if a[i] == b[j]:
            i += 1 #need to try to match next character of a
        else:
            j += 1 #will move b if no match
            
    return i == len(a) #True only if we iterated all through a

Sliding Window

size of window = right index - left index + 1

Use sliding windows when the problem:

Defines some constraint/attribute to make the subarray “valid” (valid if sum of subarray is < 10)
Asks to find subarray in some way (i.e., longest, shortest, largest valid subarray)

Examples of problems include:

Find the longest subarray with a sum less than or equal to k
Find the longest substring that has at most one “0”
Find the number of subarrays that have a product less than k

***Algorithm: Left and right bound of subarray can be defined by two pointers:

initialize two pointers left = right = 0
increment right to add new valid elements to subarray
increment left to remove elements that make subarray invalid
keep track of constraint using a variable “curr”” and then do “curr += nums[right]” etc. (to maintain O(1))
use for loop to increment right to add elements
use while loop to remove elements until array valid
update answer after exiting while loop

For an array of length n, there are:

n subarrays of length 1
(n - 1) subarrays of length 2
(n - 2) subarrays of length 3…
So in total there are $\frac{n(n+1)}{2}$ subarrays

Ex: Return len of longest subarray that sums < k:

def subarr(array,k):
    i = j = 0
    curr = 0 #constraint checker
    ans = 0
    for i in range(len(array)): #keep adding elements til
        curr += array[i] #update current checker
        while curr > k: #keep removing elements until current is <= k
            curr -= array[j]
            j += 1        
        ans = max(ans, right - left + 1)
    
    return ans

Ex:Return len of longest sequence of 1’s in an array of 1s and 0s. You may flip one 0 (notice this is the same as saying longest array that contains at most one 0):

def ones(array): #constraint in this problem is curr <= 1 zeros
    i = j = ans = 0
    curr = 0
    for i in range(len(array)):
        if array[i] == 0: #if right pointer encounters 0
            curr += 1 
        while curr > 1: #remove element if left pointer is 0
            if array[j] == 0:
                curr -= 1
            j += 1   
        ans = max(ans, right - left + 1)

    return ans

Number of Subarrays

Suppose current window is (left, right). Number of valid subarrays up till right index = len of window (because left can keep indexing until right).
Inside while loop, update answer: [Ans += current window length]

Ex: Return num of subarrays whose product < k

def subarr(array,k):
    if k <= 1:
        return 0
    
    j = answer = 0
    curr = 1
    for i in range(len(array)):
        curr *= array[i]
        while curr >= k:
            curr /= array[j]
            j += 1
        
        windowlen = i - j + 1 #if you fix the right bound, left bound can take any value up to right 
        ans += windowlen
        
    return answer

Fixed Window Size (problems that require subarrays to be some fixed length k)

build window: from index 0 to index (k -1)
add element at index i and keep window size by removing element at index (i - k)

Ex: Find sum of the subarray with the largest sum whose length is k:

def subarr(nums,k):
    curr = 0 
    for i in range(k): #build first window 
        curr += nums[i] #sum of first window
    
    ans = curr 
    for i in range(k, len(nums)): #start at element to right of existing window
        curr += nums[i] - nums[i - k] #add right and remove left element
        ans = max(ans, curr)
    
    return an

Prefix Sum

Create array prefix where prefix[i] is the sum of all elements up to i
Sum from i to j = prefix[j] - prefix[i-1] <– (which is the sum before index i)

Given int array nums, queries (pertaining to index of nums) where queries[i] = [x, y] and a limit, return bool arr true if the sum from x to y is less than limit:
nums = [1, 6, 3, 2, 7, 2]
queries = [[0, 3], [2, 5], [2, 4]]
limit = 13
the answer is [true, false, true]

def answer_queries(nums, queries, limit):
    #builds the prefix array
    prefix = [nums[0]] #start with first element in nums so [-1] index won't be empty
    for i in range(1, len(nums)): #start adding the last value of prefix with the next value in nums
        prefix.append(nums[i] + prefix[-1])
    
    ans = []
    for x, y in queries:
        curr = prefix[y] - prefix[x] + nums[x] # add nums[x] bc it's included in array 
        ans.append(curr < limit)

    return ans

Ex: Running Sum of 1d Array: Given an array of integers nums, you start with an initial positive value startValue. In each iteration, you calculate the step by step sum of startValue plus elements in nums (from left to right). Return the minimum positive value of startValue such that the step by step sum is never less than 1.

Input: nums = [-3,2,-3,4,2]
Output: 5
Explanation: If you choose startValue = 4, in the third iteration your step by step sum is less than 1.

Make prefix sum array
Find minimum of prefix array (pref_min)
Find X such that sum(X,pref_min) is 1
If X is less than 1, return 1

def minStartValue(self, nums):
        prefix = [nums[0]]
        for i in range(1,len(nums)):
            prefix.append(prefix[-1]+nums[i])

        if 1 - min(prefix) < 1:
            return 1
        return 1 - min(prefix)

2. Hashing

A hash function is a function that takes any input and converts to an integer (that is less than some determined value).

PROS

Hashmaps (dictionaries) are all O(1) for the following: adding key value pairs, delete element if exists, check existence.

CONS

slower for smaller input sizes
collisions (when different keys convert to same integer)
take up more space (arrays are more flexible with resizing)

Checking for Existence

Ex: Given an array of integers nums and an integer target, return indices of two numbers such that they add up to target. You cannot use the same index twice.

Store each (key, value) as (element, and it’s index)
Iterate through the array, checking if already exists in the dictionary
If not, initialize new entry
Else, return array[target - array[i]] (which is the index of the “target - array[i]” element)

Missing Number Ex: Given an array nums containing n distinct numbers in the range [0, n], return the only number in the range that is missing from the array.

Approach 1: Sort and compare (return the index that is out of place compared to array element when sorted ascending)
Approach 2: Hashset (see which number missing from range [0,n] after creating a dictionary)
Approach 3 (clever trick): Sum Cancellation (sum of expected minus sum of array)

Counting

General tip: Use hashmaps for anything counting related

Ex: You are given a string s and an integer k. Find the length of the longest substring that contains at most k distinct characters. For example, given s = “eceba” and k = 2, return 3. The longest substring with at most 2 distinct characters is “ece”.

Sliding windows + hashmap: Iterate through the string with sliding windows technique and update the hashmap (deleting elements from left and adding elements such that it satisfies the constraint of len(dict) <= 2)

def find_longest_substring(s, k):
    counts = {}
    left = ans = 0
    for right in range(len(s)):
        counts[s[right]] += 1 #add the letter (key) to dictionary
        while len(counts) > k: #while constraint is violated, keep removing count (value) of letter (key)
            counts[s[left]] -= 1
            if counts[s[left]] == 0: #also remove letter (key) if value is 0
                del counts[s[left]]
            left += 1 
        
        ans = max(ans, right - left + 1)
    
    return ans

Anagrams

Sorting the strings in alphabetical order, if they are anagrams they will be equal

Ex: Given an array of strings strs, group the anagrams together. For example, given strs = [“eat”,”tea”,”tan”,”ate”,”nat”,”bat”], return [[“bat”],[“nat”,”tan”],[“ate”,”eat”,”tea”]].

def groupAnagrams(self, strs):
    groups = defaultdict(list)
    for s in strs:
        key = "".join(sorted(s))
        groups[key].append(s)
    
    return groups.values()

Ex: Minimum Consecutive Cards to Pick Up: Given an integer array cards, find the length of the shortest subarray that contains at least one duplicate. If the array has no duplicates, return -1.

Initialize a dictionary storing all the indexes of the elements as values
The shortest array will have the same element in its first and last index
Check the distance between all adjacent pairs of values and find the minimum

3. Linked Lists

Even though head changes, ptr still refers to same node

ptr = head
head = head.next
head = None

Single Linked Lists
We have a single “next” pointer, so we need a reference to node at i-1 to refer to previous

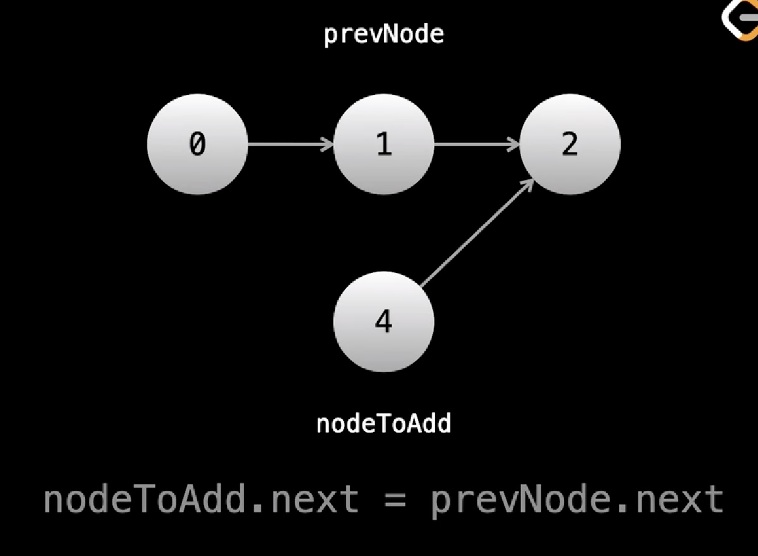
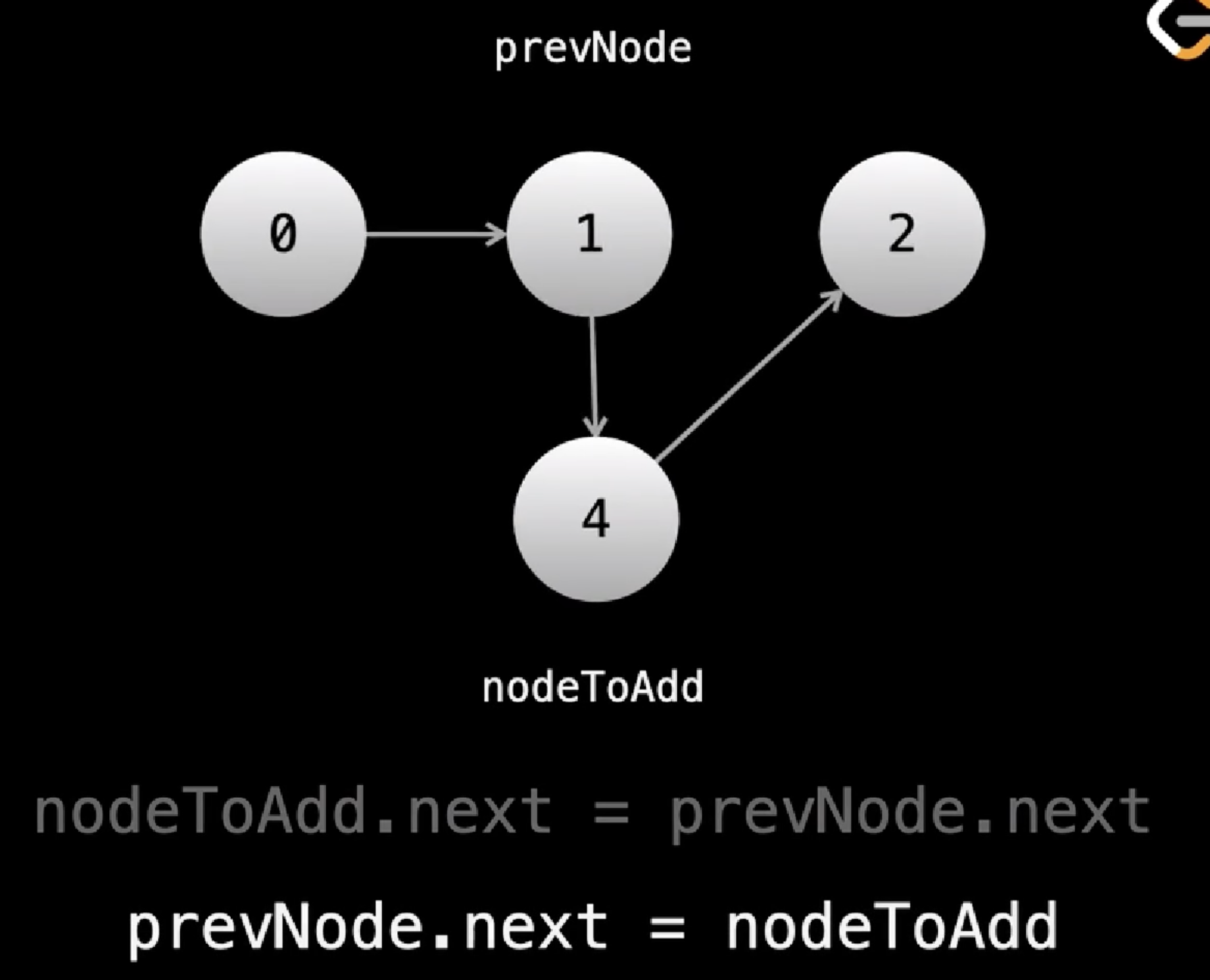
Say we want to add a new element X into position i.

We need a pointer at i-1
The next element (which is at i) will be pushed to i+1
Which becomes the next node of X
X becomes the next node of pointer We need a reference to the node at (i - 1) if we wanted to add or remove at (i)

class ListNode:
    def __init__(self, val):
        self.val = val
        self.next = None

def add_node(prev_node, node_to_add): #prev_node at i-1
    node_to_add.next = prev_node.next #
    prev_node.next = node_to_add #set the next step of the previous node at (i-1) to make it i which becomes equal to the new element 

Doubly Linked Lists
We now have a pointer to previous node as well, so unlike single lists, we only need reference to node at i.

class ListNode:
    def __init__(self, val):
        self.val = val
        self.next = None
        self.prev = None

# Let node be the node at position i
def add_node(node, node_to_add):
    prev_node = node.prev
    node_to_add.next = node
    node_to_add.prev = prev_node
    prev_node.next = node_to_add
    node.prev = node_to_add

# Let node be the node at position i
def delete_node(node):
    prev_node = node.prev
    next_node = node.next
    prev_node.next = next_node
    next_node.prev = prev_node

Linked Lists w/ Sentinel Nodes
Head pointer @ start of list and tail pointer @ end of linked lists.
The real head of the linked list is head.next and the real tail is tail.prev.
The sentinel nodes themselves are not part of our linked list.

Fast and slow pointers

If we have one pointer moving twice as fast as the other, then by the time it reaches the end, the slow pointer will be halfway through since it is moving at half the speed.

def get_middle(head):
    slow = head
    fast = head
    while fast and fast.next: #fast.next is necessary because if fast is last then fast.next is null and fast.next.next throws an error
        slow = slow.next
        fast = fast.next.next
    
    return slow.val

Ex: Checking if a linked list has a cycle/is closed (imagine a circular track)

If the fast pointer eventually meets the slow pointer at some point, we can conclude its closed
Otherwise if the distance between fast and slow just keeps increasing with no end, its non-cyclical

class Solution:
    def hasCycle(self, head: Optional[ListNode]) -> bool:
        slow = head
        fast = head
        while fast and fast.next:
            slow = slow.next
            fast = fast.next.next
            if slow == fast:
                return True

        return False

Ex: Given a linked list and an integer k, return the k’th from the tail end

Position slow pointer at head and fast pointer k steps from head.
When fast pointer reaches the end, we know slow must be k’th distance away from tail.

def find_node(head, k):
    slow = head
    fast = head
    for _ in range(k):
        fast = fast.next
    
    while fast:
        slow = slow.next
        fast = fast.next
    
    return slow

Ex: Given the head of a sorted linked list, delete all duplicates such that each element appears only once. Return the linked list sorted as well.

def duplicates(head):
    current = head
    while current and current.next:
        if current == current.next: #if there is a duplicate
          current.next = current.next.next #skip the duplicate (current.next) node
        else:
          current = current.next #increment as normal
    
    return head

Reversing Linked Lists

At any given node curr, we can set curr.next = prev to switch direction of arrow

At every step through the list (driven by next_node), we switch the directional arrow

def reverse_list(head):
  prev = Null #set prev to be before the head
  curr = head
  while curr:
      next_node = curr.next # first, make sure we set the next node one step forward
      curr.next = prev      # reverse the direction of the arrow
      prev = curr           # now prev moves forward to the start curr location
      curr = next_node      # move curr forward
        
  return prev

Ex: Swap Nodes in Pairs:

Given the head of a linked list, swap every pair of nodes. For example, given a linked list 1 -> 2 -> 3 -> 4 -> 5 -> 6, return a linked list 2 -> 1 -> 4 -> 3 -> 6 -> 5.

class Solution:
    def swapPairs(self, head: ListNode) -> ListNode:
        dummy = ListNode(0,head) #initialize dummy variable
        prev, curr = dummy, head #dummy is set to the node before head

        while curr and curr.next: 
          # first define a few pointers
          nextPair = curr.next.next
          secondNode = curr.next
          
          secondNode.next = curr #point the next step of secondNode back to curr
          curr.next = nextPair #point the next step of the first node to the next pair
          
          #now we know first node is in 2nd nodes position
          prev.next = secondNode #swap 2nd node to first position
          
          #update pointers
          prev = curr
          curr = nextPair
        
        return dummy.next #which will always point to head

4. Stacks

LIFO (last in first out) – like a stack of plates
Push = append to list
Pop = remove from end of list
Check conditions for stack[-1]

def isValid(s)
    stack = []
    matching = {"(": ")", "[": "]", "{": "}"}

    for c in s:
        if c in matching: # if c is an opening bracket
            stack.append(c)
        else: # c is either a closing bracket
            if not stack: # or it DNE so return False
                return False
            previous_opening = stack.pop() # check for matching closing bracket
            if matching[previous_opening] != c: #if does not match then return false
                return False

    return not stack # since we are popping/removing elements as we go, return True if empty

Queues

FIFO (first in first out) – like a fast food line

from collections import deque

class RecentCounter:
    def __init__(self):
        self.queue = deque()

    def ping(self, t: int) -> int:
        while self.queue and self.queue[0] < t - 3000:
            self.queue.popleft()
        
        self.queue.append(t)
        return len(self.queue)


# Your RecentCounter object will be instantiated and called as such:
# obj = RecentCounter()
# param_1 = obj.ping(t)

Monotonic

For each index, find the number of days it is away from a warmer day

class Solution:
    def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
        stack = [] #stores indices as long as temp keeps decreasing
        answer = [0] * len(temperatures) # init array
        
        for i in range(len(temperatures)):
            while stack and temperatures[stack[-1]] < temperatures[i]: #make sure stack is monotonic decreasing
                j = stack.pop() 
                answer[j] = i - j #find how many indices away it is from the element
            stack.append(i) 
        
        return answer

5. Binary Trees

Depth First Search (DFS): Travel down as deep as possible before wide

Iterative Approach (Using Stacks): Returning DFS Order

def DFS(root):
    if not root: #base case
      return []
    
    stack = [root] #initialize a stack with root node to keep track of current levels / nodes
    answer = []
    while stack: #while stack contains at least one node
        current = stack.pop() #checks last node of stack (left to right since last element being pushed is left child below)
        answer.append(current.val) #stores current node
        if current.right: #if current node has a right child, then push onto stack
            stack.append(current.right)
        if current.left: #if current node has a left child, then push onto stack
            stack.append(current.left)

Recursive Approach: Returning DFS Order

THE LINE AFTER RECURSIVE FUNCTION CALL IS ONLY EXECUTED AFTER BASE CASE IS MET
Preorder: Logic done on current node before moving onto children
Inorder: Logic done after reaching node without left child
Postorder: Logic done only after reaching leaf nodes

def dfs(node):
  if node == None:
      return #if base case is hit, return

  dfs(node.left) # RECURSIVELY KEEP CALLING LEFT UNTIL NO LEFT NODE EXISTS...THEN CALL RIGHT
  dfs(node.right)
  return

if base case is hit, return to previous node
3 and 4 is done, so go to line 5
line 5 returns back to previous node

def isSameTree(self, p, q):
        # Are both p and q None? If so, we have reached all the way to the leaf nodes
        if not p and not q:
            return True 

        # Is one of them Null? If so, the other must be a node and they are different
        if not p or not q:
            return False

        # At this point, if above criteria still have not been met, we know both are nodes
        # Are their values different?
        if p.val != q.val:
            return False

        # Recursive call to the next level down
        return self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)

Ex: Return Maximum Depth of Tree

def maxDepth(self, root):
    if not root:
        return 0
    
    left = self.maxDepth(root.left)
    right = self.maxDepth(root.right)
    return max(left, right) + 1

Breadth First Search (BFS):

Traverse as wide as possible at given level first before deep

init a queue
while queue:
init variable tracking length of queue (# of current nodes we need to iterate left/right for)
iterate over that many of times (to find left/right child of current nodes)
pop the queue so it clears for the next step
append the children (so queue only storing next nodes)

from collections import deque

def print_all_nodes(root):
    queue = deque([root])  #stores all nodes at NEXT level from left to right
    while queue:
        nodes_in_current_level = len(queue) #we must iterate over this # of times to find left/right child for each

        for _ in range(nodes_in_current_level): #iterate over each level
            node = queue.popleft() #removes all nodes at CURRENT level
    
            print(node.val)
            
            if node.left:
                queue.append(node.left)
            if node.right:
                queue.append(node.right)

Ex: Return all right values

def rightSideView(self, root):
    if not root:
        return []
    
    ans = []
    queue = deque([root])
    
    while queue:
        current_length = len(queue)
        ans.append(queue[-1].val) # this is the rightmost node for the current level
        
        for _ in range(current_length):
            node = queue.popleft()
            if node.left:
                queue.append(node.left)
            if node.right:
                queue.append(node.right)
    
    return ans

Binary Search Trees:

All left children are less than the parent, all right values are greater than the parent

Ex: Give a range [low,high], return sum of all tree values within that range

  def rangeSumBST(self, root, low, high):
      if not root:
          return 0

      ans = 0
      if low <= root.val <= high: 
          ans += root.val
      if low < root.val:
          ans += self.rangeSumBST(root.left, low, high)
      if root.val < high:
          ans += self.rangeSumBST(root.right, low, high)

      return ans

Ex: Check if its a valid binary search tree

  def isValidBST(self, root: Optional[TreeNode]) -> bool:
      def dfs(node, small, large):
          if not node:
              return True
          
          if not (small < node.val < large):
              return False

          left = dfs(node.left, small, node.val) #update the upper bound cuz left has to be smaller
          right = dfs(node.right, node.val, large) #update the lower bound cuz right has to be greater

          # tree is a BST if left and right subtrees are also BSTs
          return left and right

      return dfs(root, float("-inf"), float("inf"))

6. Graphs

Undirected (Bidirectional) vs Directed (Unidirectional)
Usually represented by a dictionary where each key is node, values are its outgoing connections from each node
Use a set “seen” to make sure node is only visited once (to prevent infinite loops in cyclical cases)

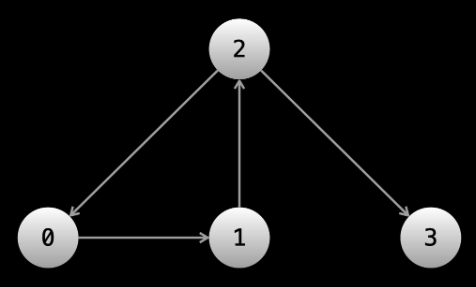
Input Type 1: Array of Edges (pairs of edges)

edges = [[0, 1], [1, 2], [2, 0], [2, 3]]
each pair element in array represents an outgoing edge connection

def build_graph(edges):
    graph = {}
    for x, y in edges:
        graph[x].append(y)
        # graph[y].append(x)
        # uncomment the above line if the graph is undirected
    
    return graph

Input Type 2: Adjacency List (index based)

graph = [[1], [2], [0, 3], []]
graph[i] = outgoing connections from node i

Input Type 3: Adjacency Matrix (matrix form of array of edges)

graph[i][j] = 1 if there is an outgoing connection from node i to node j
i.e., if graph[node][i] = 1 then i is a neighbor to node
essentially the same as putting a 1 in the position of “array of edges” representation

$$ \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{bmatrix} $$

DFS Graphs

Exploring each node’s neighbors recursively one by one

Return the total number of closed cycle loops

Init a set “seen” to prevent from revisiting nodes
Internal logic: If node[i]’s neighbor has not seen yet, then mark as seen and recursively check the neighbors on all of its neighbors (this will handle all connections in a cycle as “seen”)
Iterate over all nodes and if something hasn’t been seen yet, we know that’s a new cycle

def findCircleNum(self, isConnected: List[List[int]]) -> int:
    
  #internal logic: marks all neighbors in a province as seen
  def dfs(node): 
        for neighbor in graph[node]:
            if neighbor not in seen:
                seen.add(neighbor)
                dfs(neighbor)
    
    def dfs(start): #iteratively instead of recursively
        stack = [start]
        while stack:
            node = stack.pop()
            for neighbor in graph[node]:
                if neighbor not in seen:
                    seen.add(neighbor)
                    stack.append(neighbor)     
                  
                   
    # build the graph
    n = len(isConnected)
    graph = defaultdict(list)
    for i in range(n):
        for j in range(i + 1, n): 
        # instead of for j in i because if 1s are in the diagonal, 
        # that would just indicate a node connection to itself 
            if isConnected[i][j]:
                graph[i].append(j)
                graph[j].append(i)
    
    seen = set()
    ans = 0
    
    for i in range(n): #checks for new provinces
        if i not in seen:
            # add all nodes of a connected component to the set
            ans += 1
            seen.add(i)
            dfs(i)
    
    return ans

Ex: Return the minimum number of swaps needed for a directed graph to make them all lead into one node

Indentify all edges pointing away from 0
Start DFS starting from node 0 (meaning we will always be moving away from 0)
Record the direction, if the original direction matches the DFS, then we need +1 swap (indicate moving towards)

def minReorder(self, n: int, connections: List[List[int]]) -> int:
    roads = set()
    graph = defaultdict(list)
    for x, y in connections:
        graph[x].append(y)
        graph[y].append(x)
        roads.add((x, y))

    def dfs(node):
        ans = 0
        for neighbor in graph[node]:
            if neighbor not in seen:
                if (node, neighbor) in roads:
                    ans += 1
                seen.add(neighbor)
                ans += dfs(neighbor)
        
        return ans

    seen = {0}
    return dfs(0)

    #iterative version 
    ans = 0
    stack = [0]
    seen = {0}
    while stack:
        node = stack.pop()
        for neighbor in graph[node]:
            if neighbor not in seen:
                if (node, neighbor) in roads:
                    ans += 1
                seen.add(neighbor)
                stack.append(neighbor)
    
    return ans

Ex: rooms[i] is all keys to other rooms that can be found in that room. Return true if one can visit all rooms

def canVisitAll(rooms):
  def dfs(node):
    for neighbor in rooms[node]:
      if neighbor not in seen:
        seen.add(neighbor)
        dfs(neighbor)

  seen = set()
  dfs(0)
  return len(seen) == len(rooms)

Ex: Find islands

def numIslands(self, grid: List[List[str]]) -> int:
    def valid(row, col):
        return 0 <= row < m and 0 <= col < n and grid[row][col] == "1"
    
    def dfs(row, col):
        for dx, dy in directions:
            next_row, next_col = row + dy, col + dx
            if valid(next_row, next_col) and (next_row, next_col) not in seen:
                seen.add((next_row, next_col))
                dfs(next_row, next_col)
    
    directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
    seen = set()
    ans = 0
    m = len(grid)
    n = len(grid[0])
    for row in range(m):
        for col in range(n):
            if grid[row][col] == "1" and (row, col) not in seen:
                ans += 1
                seen.add((row, col))
                dfs(row, col)
    
    return ans

BFS Graphs

(think of water ripples from a stone in pond)

Explores all possible neighbors from starting node (level 0)
Better for finding shortest path
With BFS, every time we visit a node, we must have arrived in the fewest possible steps
Each “level” is the direct connection from the chosen node

Ex: Find shortest path of 0’s from (0,0) to (n,n)<//b>

def shortestPathBinaryMatrix(self, grid):
    if grid[0][0] == 1:
        return -1
    
    def valid(row, col):
        return 0 <= row < n and 0 <= col < n and grid[row][col] == 0
    
    n = len(grid)
    seen = {(0, 0)}
    queue = deque([(0, 0, 1)]) # row, col, steps
    directions = [(0, 1), (1, 0), (1, 1), (-1, -1), (-1, 1), (1, -1), (0, -1), (-1, 0)]
    
    while queue:
        row, col, steps = queue.popleft()
        if (row, col) == (n - 1, n - 1): #shortest path is a diagonal
            return steps
        
        for dx, dy in directions:
            next_row, next_col = row + dy, col + dx
            if valid(next_row, next_col) and (next_row, next_col) not in seen:
                seen.add((next_row, next_col))
                queue.append((next_row, next_col, steps + 1))
    
    return -1

Ex: Given the root of binary tree, target node, and integer k, return all nodes that are k distance from target from collections import deque

def distanceK(self, root, target):
  # converts tree to undirected graph
    def dfs(node, parent): 
        if not node:
            return
        
        node.parent = parent
        dfs(node.left, node)
        dfs(node.right, node)
    
    dfs(root, None)
    queue = deque([target]) #stores node at each level
    seen = {target}
    distance = 0 #ensures queue is at the kth level
    
    while queue and distance < k:
        current_length = len(queue)
        for _ in range(current_length): #iterate over all nodes at current level
            node = queue.popleft()
            for neighbor in [node.left, node.right, node.parent]: #all neighbors of tree
                if neighbor and neighbor not in seen:
                    seen.add(neighbor)
                    queue.append(neighbor)
        
        distance += 1
    
    return [node.val for node in queue]

Ex: Find distance from 0 for each cell (i.e., Return matrix of values where each cell is k distances away from 0

Start at all 0 nodes
Set all direct neighbors = 1, neighbors of neighbors = 2, and so on

def updateMatrix(self, mat):
    def valid(row, col): #check if in bounds and valid
        return 0 <= row < m and 0 <= col < n and mat[row][col] == 1
    
    m = len(mat)
    n = len(mat[0])
    queue = deque()
    seen = set()
    
    for row in range(m):
        for col in range(n):
            if mat[row][col] == 0:
                queue.append((row, col, 1))
                seen.add((row, col))
    
    directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]

    while queue:
        row, col, steps = queue.popleft()
        
        for dx, dy in directions:
            next_row, next_col = row + dy, col + dx
            if (next_row, next_col) not in seen and valid(next_row, next_col):
                seen.add((next_row, next_col))
                queue.append((next_row, next_col, steps + 1))
                mat[next_row][next_col] = steps
    
    return mat

7. Heaps

Used for repeatedly finding max or min element
Complete binary tree structure (all levels must be full except last)

Min Heapify:

Starts at the last nonleaf node
Take min of (child 1, child 2, parent)
Swap places with the min as the parent
Keep doing this until we reach the root node which should then contain the min value

Ex: Stones[i] is the weight of i’th stone. Choose heaviest two stones x and y. If x == y, both stones removed. If x < y, put back a stone with weight y - x. Return weight of the last remaining stone.

import heapq #min to max, heapop pops the min

def lastStoneWeight(stones):
        stones = [-stone for stone in stones] #bc heapq only does min heaps, take the negative for the max heap
        heapq.heapify(stones) # turns an array into a heap in linear time
        while len(stones) > 1:
            first = abs(heapq.heappop(stones)) #pop heaviest stone
            second = abs(heapq.heappop(stones)) #pop second heaviest stone
            if first != second:
                heapq.heappush(stones, -abs(first - second)) #push back the difference

        return -stones[0] if stones else 0

Two Heaps

Good for finding the median

Ex: Find median

Max heap with lower half of data
Min heap with upper half of data
If even: Heappop average of both will return the median
If odd: Heappop element of larger array is the median
1. Push num onto the max heap (as mentioned above we arbitrarily chose the max heap).
2. Pop from the max heap, and push that element onto the min heap.
3. After step 2, if the min heap has more elements than the max heap, pop from the min heap and push the result onto the max heap.

def __init__(self):
    self.min_heap = []
    self.max_heap = []

def addNum(self, num):
    heapq.heappush(self.max_heap, -num) #add num to max heap
    heapq.heappush(self.min_heap, -heapq.heappop(self.max_heap)) #pop from max heap and push to min heap
    if len(self.min_heap) > len(self.max_heap): #if odd
        heapq.heappush(self.max_heap, -heapq.heappop(self.min_heap)) #balances out

def findMedian(self):
    if len(self.max_heap) > len(self.min_heap): #the popped element of larger array is the median, otherwise it's the average
        return -self.max_heap[0]
    return (self.min_heap[0] - self.max_heap[0]) / 2

Top K

We want to find the “best” k elements of a collection
Use heap to keep popping off the “worst” elements to keep the top K elements in answer array

def topKFrequent(nums,k):
    counts = {}
    heap = []
    
    for key, val in counts.items():
        heapq.heappush(heap, (val, key))
        if len(heap) > k: #keep popping off worse elements
            heapq.heappop(heap)
    
    return [pair[1] for pair in heap]

8. Greedy Approaches

Makes locally optimal decision at each step without accounting for future rewards
Usually will ask for max or min of something

Ex: Integer array arr and an integer X. If X < array[i], then X is destroyed. Else if X >= array[i], then X += array[i]. Return True if X can be greater than all elements in array

def asteroidsDestroyed(array, X):
    array.sort() #smallest to largest
    for i in array:
        if i > X: #return false if any element is greater than X 
            return False
        X += i  #otherwise, add i to X
    
    return True

Ex: Min # of subsequences needed where all elements inside each have max deviation of k

def solution(array, k)
    subsets = 0
    array.sort()
    minimum = array[0] #smallest element
    for i in range(1, len(array)):
        if array[i] - minimum > k: #if the max difference is greater than k 
            minimum = array[i]
            subsets += 1
    
    return subsets

Ex: You are given n projects with arr profits and arr minimum capital required. You start with w capital. Completing a project gives you w += profits[i]. Return max w possible if you are allowed k projects.

Create a max heap for profits that satisfy your capital w
Pop off the project you can do with max profits you can take on for each project

import heapq

def findMaximizedCapital(k, w, profits, capital):
    n = len(profits)
    projects = sorted(zip(capital, profits)) 
    heap = []
    i = 0
    
    for _ in range(k):
        while i < n and projects[i][0] <= w:
            heapq.heappush(heap, -projects[i][1])
            i += 1
        
        if len(heap) == 0:
            # not enough money to do any more projects
            return w
        
        # minus because we stored negative numbers on the heap
        w -= heapq.heappop(heap)
    
    return w

9. Binary Search

Worst case runs O(log n)
Usually space needs to be sorted prior
Divides each section in half recursively

Ex: We want to find index of X in a sorted array. 1) Start in the middle of a sorted array. If the middle is less than X, then throw away the lower half. Do this iteratively.

Implementation:

left = 0
right = len(arr) - 1

while left <= right:
    mid = (left + right) // 2 #check middle element
    if arr[mid] == x: #then the element has been found, return.
        return mid 
    if arr[mid] > x: #then throw away top half: lower the upper bound to the midpoint (excluding)
        right = mid - 1.
    else arr[mid] < x:  #throw away bottom half: raise lower bound to midpoint
        left = mid + 1
#if you get to this point without arr[mid] = x, then the search was unsuccessful. 
# The left pointer will be at index where x would need to be inserted to maintain sort
return left

Ex: We want to find index of X in a sorted matrix

(row = i // items in each row)
(column index = i % items in each row)
index i has position (m, n) = (i // n, i % n)
since there are n items in each row, we know that at index i, we’ve passed by n * _ = i elements
and the column index “resets” every n elements, so we need i % n

def searchMatrix(matrix, target):
    m, n = len(matrix), len(matrix[0])
    left, right = 0, m * n - 1 #right pointer flattens matrix into array
    
    while left <= right:
        mid = (left + right) // 2
        row = mid // n
        col = mid % n
        num = matrix[row][col]
        
        if num == target:
            return True
        
        if num < target:
            left = mid + 1
        else:
            right = mid - 1
    
    return False

Ex: Find the number of candies each person can eat without exceeding their calorie limits

Use prefix sum
Returning the left pointer tells us the max we reach before exceeding limit

def eatCandies(candies, calorieLimits):
    candies = sorted(candies)
    
    prefix = [candies[0]]
    for i in range(1, len(candies)):
        prefix.append(candies[i] + prefix[-1])
    
    # Process each calorie limit
    results = []
    for limit in calorieLimits:
        left = 0
        right = len(prefix) - 1
        while left <= right:
            mid = (left + right) // 2
            if prefix[mid] <= limit:
                left = mid + 1
            else:
                right = mid - 1
        
        results.append(left) #returning left tells you the max you can go before exceeding limit (how far you can go down the line of candies)
    
    return results

Implementation Tips

Return left to find minimum
Return right to find maximum

10. Backtracking

Pruning non-solution paths to reduce the possibility space
Good for problems where you want to “find all” of something
Hint: If the input constraint is very small n <= ~15
1. calling recursive backtrack() = moving to child of node
1. remove modification = moving back to parent node

Template
UNDO MODIFICATION; LINE AFTER RECURSIVE CALL IS ONLY EXECUTED AFTER BASE CASE

#let curr represent the thing you are building
#it could be an array or a combination of variables
def backtrack(curr):
    if base case:
        increment / add to ans
        return

    for i in input:
        modify curr
        backtrack(curr) #recursion ends only after base case
        undo whatever modification was done to curr

Ex: Find all permutations of array

def permute(nums):
    def backtrack(curr):
        if len(curr) == len(nums):
            ans.append(curr[:]) #shallow copy curr so it's not mutable by ###ref###
            return
    
        for num in nums:
            if num not in curr: #only options left are the other values
                curr.append(num) ###ref###
                backtrack(curr) #moving to the child node
                             
                #only AFTER recursion meets base case, then we end here with curr.pop()
                curr.pop() #moving back to the parent node
        
    ans = []
    backtrack([])
    return ans

Ex: Find all subsets of array

We do not want duplicates so only consider any number that comes AFTER that value

def subsets(nums):
    def backtrack(curr, i):
        if i > len(nums): #if index is out of bounds
            return

        ans.append(curr[:]) #append copy of current subset
        for j in range(i, len(nums)):
            curr.append(nums[j]) #add nums[j] to current subset
            backtrack(curr, j + 1) #recurse with next index
            curr.pop() #remove last element to backtrack

    ans = []
    backtrack([], 0)
    return ans

Ex: N-Queens Find number of unique solutions to place n queens on an n x n chessboard

We need to use backtracking to figure out all possible placements (if the next step doesn’t work, go back to previous)
We need to figure out which row, col, diagonol, antidiagonal is free

***HACK 1: Each diagonal has the same (row - col) value because moving down and right, both row and col gets incremented so difference is same throughout

***HACK 2: Each antidiagonal has the same (row + col) value because moving down increments row and left decrements col so sum is preserved

def totalNQueens(n):
    def backtrack(row, diagonals, anti_diagonals, cols):
        # Base case - N queens have been placed
        if row == n: #if we have managed to reach the last row (after placing one queen on each)
            return 1

        solutions = 0
        for col in range(n):
            curr_diagonal = row - col
            curr_anti_diagonal = row + col
            # If the queen is not placeable on the col, diag, or antidiag then check other squares
            if (col in cols 
                  or curr_diagonal in diagonals 
                  or curr_anti_diagonal in anti_diagonals):
                continue 

            # Otherwise its safe to "Add" the queen to the board
            cols.add(col) 
            diagonals.add(curr_diagonal)
            anti_diagonals.add(curr_anti_diagonal)

            # Move on to the next row with the updated board state
            solutions += backtrack(row + 1, diagonals, anti_diagonals, cols)

            # "Remove" the queen from the board since we have already
            # explored all valid paths using the above function call
            cols.remove(col)
            diagonals.remove(curr_diagonal)
            anti_diagonals.remove(curr_anti_diagonal)

        return solutions

    return backtrack(0, set(), set(), set())

11. Dynamic Programming

Optimize recursion with memoization (storing results in hashmap to avoid repeated computations)

Problems using DP will have 2 traits:

Asking for an optimal value (max/min) of something, or the # of ways to do something
At each step, you need to make decision that affects future decisions

Ex: Fibonacci with memoization

def fibonacci(n):
    if n == 0:
        return 0
    if n == 1:
        return 1

    if n in memo:
        return memo[n]
    
    memo[n] = fibonacci(n - 1) + fibonacci(n - 2)
    return memo[n]

memo = {}

Framework for DP

Ex: Min Cost Climbing Stairs: You are given an array where array[i] is the cost of the i’th step. Once you pay, you can either go up one of two steps. Find min cost to reach top

1. We need a function/data structure to compute answer:

What is the function returning? (Returning the cost up to the i’th step)
What are the state inputs? (We need the i’th step as the state)
- so lets have dp(i)

2. We need a recurrence relation for state transitions:

Say we want to compute min cost to step 100
We know we needed to arrive from step 98 or 99
So dp(100) = min(dp(99) + cost[99], dp(98) + cost[98])
we know dp(99) returns the min cost of getting to 99’th step and dp(98) returns min cost to get to 98’th step
So dp(i) = min(dp(i-1) + cost[i-1], dp(i-2) + cost[i-2])

3. We need a base case:

We start at steps 0 or 1 (which means cost is 0)
So dp(0) = dp(1) = 0

def minCostClimbingStairs(self, cost: List[int]) -> int:
    # 1. A function that returns the answer
    def dp(i):
        if i <= 1:
            # 3. Base cases
            return 0
        
        if i in memo:
            return memo[i]
        
        # 2. Recurrence relation
        memo[i] = min(dp(i - 1) + cost[i - 1], dp(i - 2) + cost[i - 2])
        return memo[i]
    
    memo = {}
    return dp(len(cost))

Ex: Robbing Houses: array[i] represents how much money you gain from robbing house i. You cannot rob houses directly next to one another (so you can only skip one house). Return max amount you can rob

What is the input? –> the index i of the house
What is the output? –> the max amount of money we get up to house i
What is the recursive relation? –> at each index, we either don’t rob the current house because we robbed the previous house dp(i-1) OR we robbed the prev.prev house plus the current house so array[i] + dp(i-2)
What is the base case? –> we rob either the first so dp(0) = array[0] or go to the second to see if it’s more than the first dp(1) = max(array[0], max[array[1]). We need dp(1) otherwise the recurrence relation will use dp(-1).

from functools import cache

def rob(houses):
    @cache #python memoization
    def dp(i):
        if i == 0:
            return houses[0]
        if i == 1:
            return max(houses[0], houses[1])
        else:
            return max(dp(i-1), houses[i] + dp(i-2))

    return dp(len(houses) - 1)

Hacks:

Flip between 1 and 0 is f(x) = 1 - x. f(1) = 0 and f(0) = 1.