math proofs | Chelsea Zou

Preliminary

Natural numbers $\mathbb{N}$ = {0,1,2,3…}
Integers $\mathbb{Z}$ = {…,-1,0,1,…}
Rational numbers $\mathbb{Q}$ = {$\frac{p}{q}$ where p,q $\in$ $\mathbb{Z}$ and q $\neq$ 0}
$\mathbb{R}$ is both an open interval (noninclusive) and a closed interval (inclusive).

Sets

Def: X is a proper subset $\subsetneq$ of Y if $X \subset Y$ and $X \neq Y$

Def: The empty set $\emptyset$ is the set with no elements; it is true that $\emptyset \subset X$ for any set X

Def: X and Y are disjoint if $X \cap Y = \emptyset$

Def: The Cartesian product (direct product) of X and Y is the set of ordered pairs $\{ (x,y) | x \in X$ and $y \in Y \}$. More generally, $\prod_{i=1}^{n} X_i$ = $\{ (x_1, x_2, \ldots, x_n) \mid x_i \in X_i, \ 1 \leq i \leq n\}$. $X^n$ denotes the Cartesian product of a set X for n times.

Def: Floor/ceiling. $\lceil n \rceil$ is the set of natural numbers (0,1,2…, n-1) less than n

Order of set operations matter: if X and Y are disjoint, $(X \cap X) \cup Y \neq X \cap (X \cup Y)$

Functions

Let $f: X \rightarrow Y$ be a function mapping elements from set $X$ to set $Y$.

The same X cannot map to different Y
Different X can map to same Y

For instance, Let $f: \mathbb{Z} \to \mathbb{R}$ be given by $f(x) = x^2$.
Not every R is assigned to a number in Z.
Tho different R can map to same Z (i.e., R = -2, 2).

Def: The image of x, f(x) for $x \in X$ is the element of Y that f assigns to x.

Def: The graph of a function is just the domain paired with it’s range (but not every element of Y is used up) $\{ (x,y) | x \in X$ and $f(x) = y \}$. graph(f) $\subset X \times Y$

Ex: the empty function is the function with empty graph (a graph that is the empty set of f). So $f: \emptyset \to Y$.
Let $f: X \rightarrow Y. Z \subset X \times Y$. Z is a the graph of f if:
1. for any $x \in X, \exists y \in Y \mid (x,y) \in Z$ (i.e., every vertical line through X cuts the graph at least once)
2. if (x,y) is in Z, and (x,z) is in Z, then y = z (i.e., every vertical line through X cuts the curve at most once)

Def: X is the domain, Y is the codomain (which accounts for all possible outputs, different than the range which is what actually comes out)

Ex: Let $f: \mathbb{N}\to \mathbb{N}$ be defined by $f(n) = n^2$. Let $g: \mathbb{N}\to \mathbb{R}$ be defined by $g(x) = x^2$.
– Then graph(f) = graph(g), but f and g are different functions.
Let $h: \mathbb{R}\to \mathbb{R}$ be defined by $h(x) = x^2$.
– Then graph(f) $\subsetneq$ graph(h).

Def: The range (basically the function’s outputs) is the set of images of elements in X under f; it is a subset of the codomain.

Def: f is a real-valued function if Ran(f) $\subset \mathbb{R}$

Injections, Surjections, Bijections

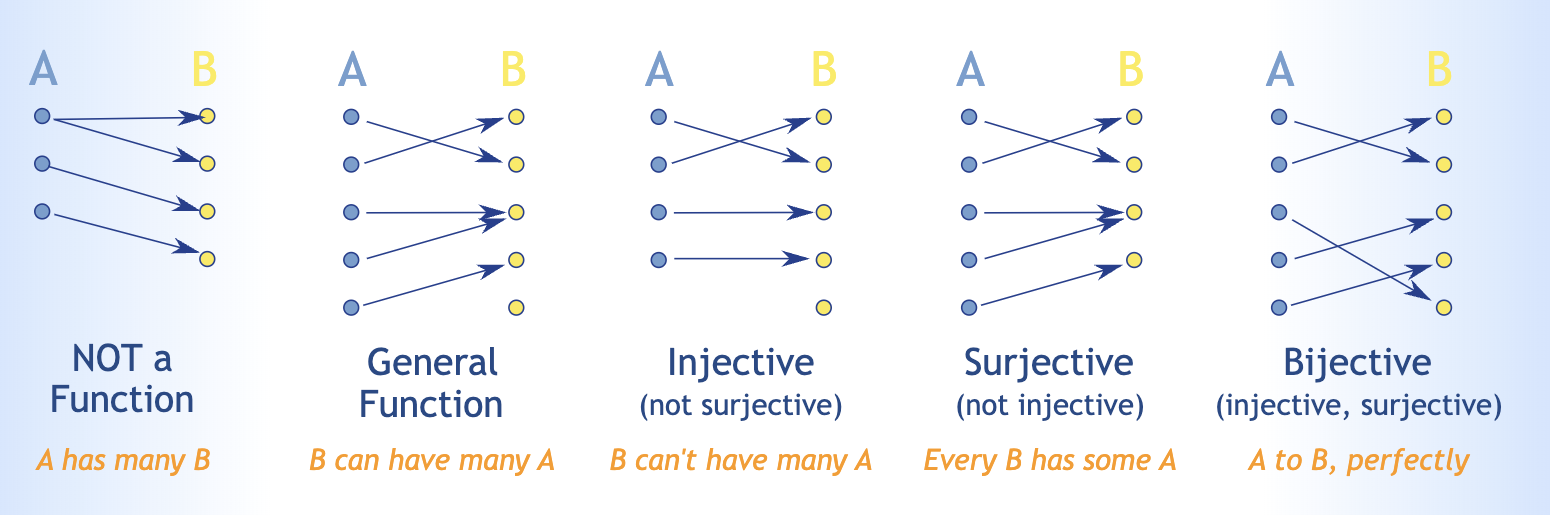
inj,surj,bij

1. Injections (one to one): Every unique x maps to a unique y; but not every y may be assigned an x

f is an injection if x & y are distinct elements $\in$ X, f(x) $\neq$ f(y).
or if f(x) = f(y) then x = y

Counterexample: $f(x) = x^2$ is not an injection bc f(-2) = f(2)
Let $f: X \to Y$ and $g: Y \to Z$. Prove that if f & g are injective, then g $\circ$ f is injective.
Proof: Suppose $g \circ f(x) = g \circ f(y)$. If g is injective, then f(x) = f(y). If f is injective, then x = y. So g $\circ$ f is injective.

2. Surjections (onto): All y must be assigned some x; even if different x maps to same y

f is a surjection if Ran(f) = Y (i.e., the range captures ALL of the codomain)

Let $Y = \{x \in \mathbb{R} \mid x \geq 0 \}$ and $f: \mathbb{R} \to Y$ be defined by $f(x) = x^2$. Prove that f is a surjection.
Proof: We need to prove that Ran(f) = Y. Since Ran(f) is always $\subset$ Y, we also want to show Y $\subset$ Ran(f). Let y $\in$ Y, so y is a non-negative real number. Then $\sqrt{y} \in \mathbb{R}$ and f($\sqrt{y}$) = y. So y $\in$ Ran(f). Since y is an arbitrary element of Y, then Y $\subset$ Ran(f).
Explanation: We start with the definition of a surjection, which is Y = ran(f). To prove equivalence, we can show that they are subsets of each other. Using the known fact that the range is always a subset of the codomain, we additionally need to show that this given codomain Y is a subset of the range. We choose some input $\sqrt{y}$ that satisfies $\in \mathbb{R}$, and the output image is y. So y is an element of Ran(f). Since y is arbitrary, this shows that every element in Y is in Ran(f), so Y $\subset$ Ran(f).

3. Bijections (both inj + surj): All elements of y must have a unique x

Bijective functions preserve key structural features of the domain, and we can treat domain and codomain as the same set.

Def: A permutation of set X is a bijection $f: X \hookrightarrow X$

Images and Inverses

Def: Inverse (Pre) Image. Let $f: X \to Y$ and $b \in Y$. The inverse image $f^{-1}(b) = \{x \in X \mid f(x) = b\}$ (Sort of like a reverse mapping)

If $b \notin Ran(f)$ then $f^{-1}(b) = \emptyset$
If f is injection, then for any $b \in Ran(f), f^{-1}(b)$ has a single element (bc injections = for every unique x $\exists$ unique y so the reverse mapping must have only a single element)

Def: Inverse Function. If $f: X \to Y$ is a bijection, then the inverse function is $f^{-1}: Y \to X$ with the graph $\{(b,a) \in Y \times X \mid (a,b) \in graph(f)\}$.

Def: Identity Function. If f is a bijection, then $f^{-1} \circ f = Id(X)$ and $f \circ f^{-1} = Id(Y)$.

Def: Restricted Domain (Considers a new function on smaller domain if non-invertible): Because some functions are not injections ($f = x^{2}$) and non-invertible (since one Y can map back to two different X’s), we can first consider a new function $g$ equal to $f$ on a subset of the domain. For instance $g(x) = x^{2}$ with domain $\{x \in R \mid x \geq 0\}$.

Ex: Let $f: X \to Y$ and $W \subset X$. The restriction of f to W is $f\vert_W = f: W \to Y$
$graph(f\vert_{W}) = graph(f) \cap [W \times Y]$

Sequences (a list of objects)

Def: A Finite Sequence $\braket{a_n \mid n < N}$ is a function with domain $\lceil N \rceil$ where $N \in \mathbb{N}$.
An Infinite Sequence is just $\braket{a_n \mid n \in N}$ (the domain is the infinite in $\mathbb{N}$)

Often denoted $\braket{a_n}$

Def: A finite Binary Sequence is a function $f:\lceil N \rceil \to \lceil 2 \rceil$, and infinite binary sequence is just $f: \mathbb{N} \to \lceil 2 \rceil$.

Def: An Infinite Union is $\bigcup_{n=1}^{\infty} X_n = \{x \mid \text{for some } n \in \mathbb{N^+}, x \in X_n\}$

collection of all elements that are in at least one of the sets $X_n$
$\mathbb{N^+}$ is the Index Set for the union

Def: Family of Sets. Let A be a set, for $a \in A$, let $X_a$ be a set ($X_a$ is a set indexed by A). $F = \{X_a \mid a \in A \}$ is the family of sets indexed by A.

Ex: Let $X_n = \{n+1, n+2,..., 2n\}$ for $n \in \mathbb{N^+}$. Then $\bigcap_{n=1}^{\infty} X_n = \emptyset$

Exercises

Prove Demorgans Laws: $(A \cap B)^c = A^c \cup B^c$
- Let $x \in (A \cap B)^c$
- Then $x \notin (A \cap B)$
- $x \notin A$ and $x \notin B$
- So $x \in A^c$ and $x \in B^c$
Prove that $A \cap (B \cup C) = (A \cup B) \cap (A \cup C)$
- Let $x \in A \cap (B \cup C)$
- $x \in A$ and $x \in (B \cup C)$
- $x \in A$ and either $(x \in B)$ or $(x \in C)$
- either $(x \in A$ and $x \in B)$ or $(x \in A$ and $x \in C)$
- ($x \in A$ and $B$) or ($x \in A$ and $C$)
- So $x \in (A \cap B) \cup (A \cap C)$

Relations

Def: A Relation from X to Y is a subset of X $\times$ Y. Any set of ordered pairs is a relation.

$xRy$ denotes that x bears a relation R to y, aka $(x,y) \in R$.
X and Y can be the same set, then the relation is “on” rather than “between”
A function $f: X \to Y$ can be thought of as a special relation from X to Y with the property that every X occurs exactly once as a first element of a pair in the relation (where no same X can map to a different Y).

Properties of Relations

Reflexive implies $(xRx)$. (2 = 2)
Symmetric implies $(xRy = yRx)$. (3 $\neq$ 2 implies 2 $\neq$ 3)
Antisymmetric implies $(xRy$ and $yRx \to x = y)$. (x $\leq$ y and x $\geq$ y implies x = y)
Transitive implies $(xRy$ and $yRz \to xRz)$. (2 < 3 and 3 < 4 implies 2 < 4 )

Orderings

Def: R is a Partial Ordering ($\preceq$) if it is:

Reflexive
Antisymmetric
Transitive

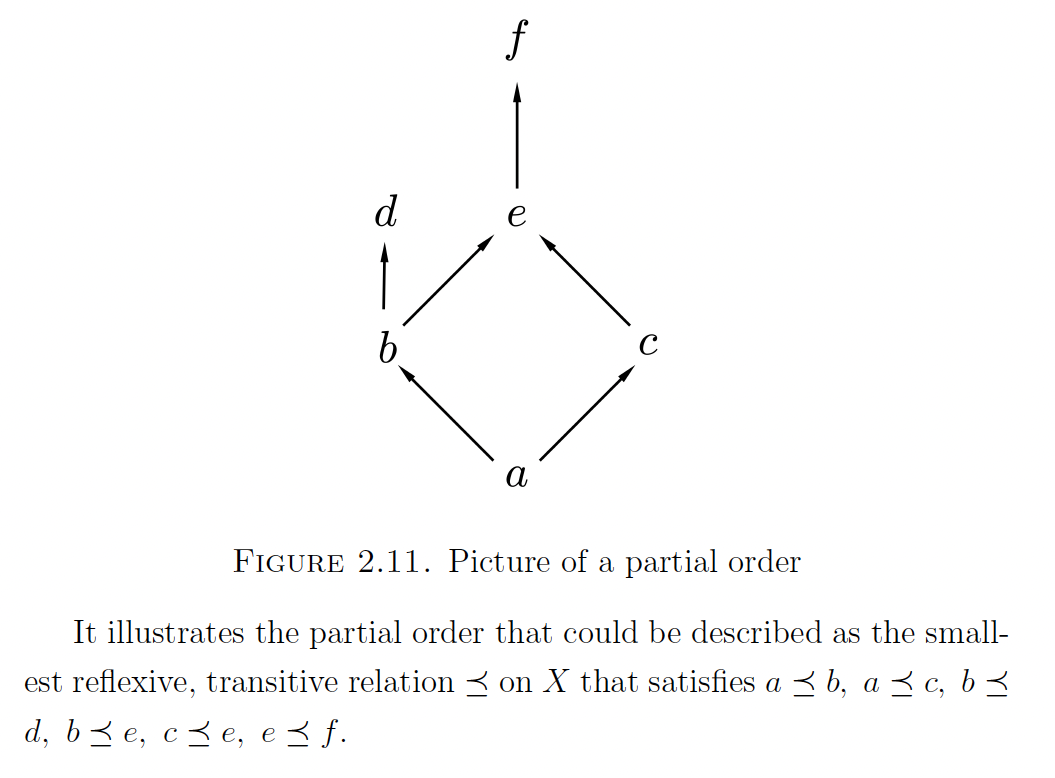
partord

Visualize partial orderings by imagining arrows connecting distinct elements $a,b$ if $a \preceq b$ and there is no third element $c$ s.t. $a \preceq c \preceq b$

Ex: Let X be a set of collections of apples and oranges (X = {$basket_a, basket_b$}). If $basket_a$,$basket_b$ are in X, then $basket_a$ $\preceq$ $basket_b$ if number of apples in $basket_a \leq basket_b$ AND number of oranges in $basket_a \leq basket_b$, this is a partial ordering.
Ex: $\subset$ is a partial ordering bc (1) Every set is a subset of itself, (2) If X is a subset of Y and vice versa, then X = Y, and (3) If X is subset of Y and Y is subset of Z then X is subset of Z.

Def: Let R be a partial ordering on X. R is a Linear Ordering (total ordering) if for any $x,y \in X$, either $xRy$ or $yRx$ (either $x \leq y$ or $y \leq x$ or both if x = y)

Ex: $\leq$ and $\geq$ on $\mathbb{R}$ is a linear ordering but $<$ or $>$ is not

Equivalence Relation

Def: Equivalence Relation (x ~ y for xRy) Basically rules that allows us to relate objects in a set that we consider the same in given context (like relating ppl with the same height from two diff groups). if R is:

Reflexive
Symmetric
Transitive

Ex: If $a,b,c,d \in \mathbb{Z}$, $(a,b) R (c,d)$ iff. $a + d = b + c$, R is an equivalence relation:
1. Reflexive: So (a,b) R (a,b) if a + b = a + b
2. Symmetric: Suppose (a,b) R (c,d) so a + d = b + c. To see if (c,d) R (a,b), check whether c + b = d + a, this holds by commutativity of addition.
3. Transitive: Suppose (a, b) R (c, d) and (c,d) R (e,f). Check (a, b) R (e,f) aka a + f = b + e. We have a + d = b + c and c + f = d + e, and adding these two we get a + d + c + f = b + c + d + e and cancelling c + d we get a + f = b + e.

Def: Equivalence Class $[x]_R$ is the set of all elements in X that satisfies some equivalence relation R for $x \in X$ (like relating heights, ages, birthdays, weights). If $y \in [x]_R$, y is a representative element.

Ex: Let X = $\{1,2,3,4,5\}$. Let R = $\{(a,b) \mid a+b \text { is even} \}$
1. First we must confirm R is an equivalence relation.
2. Equivalence class of [1] = {1,3,5}
3. Equivalence class of [2] = {2,4} and so on

Def: The set of all equivalence classes $\{[x]_R \mid x \in X\}$ is the quotient space of X by R, denoted $X/R$.

Prop: Let $x,y \in R$. If $x \sim y$, then [x] = [y]. Else, $[x] \cap [y] = \emptyset$.

Let x and y be people with same height. Then the equivalent class of person x (which is all people with same height as x) must equal to all persons with same height of person y

Def: Pairwise Disjoint: Let $\{ X_a \mid a \in A \}$ be a family of sets. The family is pairwise disjoint if for any $a,b \in A, a \neq b$ where $X_a \cap X_b = \emptyset$.

Basically, the two sets don’t overlap

Def: Partition: All and only the pairwise disjoint sets make up the partition space.A partition is a chunk of that space.

Thm: Let X be a set and ~ an equivalence relation on X. Then X/~ (quotient space of X by ~) is a partition of X (bc quotient space is just the set of all equivalence classes

Let X be a bunch of ppl and ~ is those with same height. Then X/~ (the quotient space i.e., the set of all people with the same height) is a partition (chunk) of X.

Constructing Bijections

Let $f: X \to Y$ and ~ is the equivalence relation on X induced by f. $X/f$ is the set of equivalence classes induced by ~ of X.

$X/f$ is the inverse image of an element in $Ran(f)$. If $x \in X$ and $f(x) = y$:
\[[x] = f^{-1}(y)\]
$X/f = {f^{-1}(y) \mid y \in Ran(f))}$$. The elements in X/f are level sets of f (think of topographical map where a point maps to a specific altitude (level curve), which are subsets of level sets)