stock price prediction using RNNs
building a simple web app for direct forecasting of stock prices using recurrent neural networks (RNNs)
Objective: Predict stock price for the next N days into the future.
Ingredients
- Flask,
- AlphaVantage API
- ML libraries (tensorflow, sklearn, etc.)
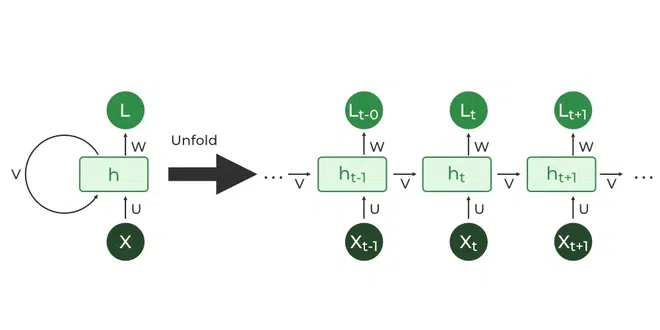
I’ll be using an RNN to predict stock prices based on the past 60 days of stock price data. Note that weights and biases are going to be the same for each iteration unit of the RNN. However, when training on long-range dependencies, RNNs can suffer from the exploding/vanishing gradients problem. Exploding gradients cause extremely large learning steps during backprop so it would bounce around alot. Conversely, vanishing gradients cause extremely tiny steps before it finds the optimal parameters. Therefore, I’ll be using an LSTM, which can prevent these problems by a modification to the hidden layer that enables RNNs to remember inputs over a longer time period.
To summarize, there are 5 components of an LSTM:
- Cell state: internal memory of the cell storing both STM and LTM
- Hidden state: the output wrt to current input, current state, and previous hidden state
- Input gate: weight of current input on current state
- Forget gate: weight of previous state on current state
- Output gate: weight of current state output into hidden state
An LSTM uses tanh and sigmoid activation functions.
- Sigmoid: \(f(x) = \frac{e^x}{e^x+1} \rightarrow (0,1)\)
- Tanh: \(f(x) = \frac{e^x - e^-x}{e^x - e^-x} \rightarrow (-1,1)\)
Sigmoid is used in the in, out, and forget gate, which removes info by squashing values to 0, and keeping info with 1. Tanh is used to update the cell state and output the hidden state, creating candidate values between -1 and 1 that scale and normalize values.
ML Model
1. Data Preprocessing
To retrieve the data, I’m using the free AlphaVantage API to get the most recent prices of any stock. First, I’ll fill in any missing values with the last known price (note that there are many different approaches to impute for missing data). I’m also applying log transform to the prices because it can better capture relative percentage changes in prices. For instance, a stock going from 10$ to 20$ should not be weighed the same as a stock going from 100$ to 110$ (weber’s law!). Finally, normalize the data using min max scaling so that the range of values fall between 0 and 1.
import requests
def preprocess(ticker):
url = f"https://www.alphavantage.co/query?function=TIME_SERIES_DAILY&symbol={ticker}&outputsize=full&apikey=Y8ZR7HEZ95DQQ9QH"
r = requests.get(url)
d = r.json()
d1 = d['Time Series (Daily)']
sorted_data = sorted(d1.items()) #ascending order
last_date = [sorted_data[-1][0]] #retrieves the last date
data = []
for index, (date, values) in enumerate(sorted_data):
close = float(values['4. close'])
if close == 0:
data.append(data[index - 1]) #imputes missing value with last known price
data.append(close)
data = np.log(np.array(data) + 1) #log transform
scaled = [ ((i - min(data)) / (max(data) - min(data))) for i in data ] #min max scaling
return scaled, last_date, max(data), min(data)
I want to create sets of 60 day batches to predict the price of next day. After doing so, I’ll split the data into training and testing to see how to well the model performs, and tweak accordingly.
from sklearn.model_selection import train_test_split
scaled, last_date, max, min = preprocess(ticker)
X = []
y = []
for i in range(60,len(scaled)):
X.append(scaled[i-60:i])
y.append(scaled[i])
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)
2. Building the Model
Now, to build the LSTM network. I’ll use the most basic architecture, but note there are fancier things you can do (such as adding attention modules, etc). There’s two LSTM layers with 50 nodes each. I’m also adding dropout and batch norm to prevent the data from overfitting.
from keras.models import Sequential
from keras.layers import LSTM, Dense, BatchNormalization, Dropout
model = Sequential()
model.add(LSTM(50, return_sequences=True, input_shape=(np.shape(X_train)[1], 1)))
model.add(LSTM(50))
model.add(Dropout(0.2))
model.add(BatchNormalization())
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
3. Training and Evaluating the Model
I’m going to be using MAE and MSE to evaluate my model performance. MAE is just the average deviation of the true values from predicted values. RMSE is the root of the average of squared errors. The difference between the two is that MAE is not very sensitive to outliers because large deviations are weighted linearly, so they do not influence the overall error as much as in the RMSE.
- MAE = \(\frac{1}{n} \sum_{i=1}^{n} \mid y_i - \hat{y}_i \mid\)
- RMSE = \(\sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2}\)
from sklearn.metrics import mean_absolute_error, mean_squared_error
model.fit(X_train, y_train, epochs=100, batch_size=32)
X_test = np.array(X_test)
y_test = np.array(y_test)
test_loss = model.evaluate(X_test, y_test)
y_pred = model.predict(X_test)
mae = mean_absolute_error(y_test, y_pred)
rmse = mean_squared_error(y_test, y_pred, squared=False)
print("Test Loss: ", test_loss)
print("Mean Absolute Error: ", mae)
print("Root Mean Square Error: ", rmse)
When I ran this, I got Test Loss: 0.0002112429210683331, Mean Absolute Error: 0.009415658948740935, Root Mean Square Error: 0.014534198440214904. Good enough. A general practice is to retrain the network on the entire dataset once you are ready to deploy your model.
4. Prediction
Now that the model is trained, I can use the last 60 days to predict the next day’s price. Remember that at the beginning, I did a log transform and min max scaling to the values. So now I’ll reverse the process and do an inverse transformation to output the actual stock price per share.
import math
def inverse_predict(last60,max,min):
y_pred = model.predict(np.expand_dims(last60, axis=0))
inverse_scaled = (y_pred[0][0]) * (max - min) + min #inverse min max scaling
prediction = math.e ** (inverse_scaled) - 1 #inverse log transform
prices_pre = np.array(last60) * (max - min) + min #inverse min max scaling
prices = math.e ** (prices_pre) - 1 #inverse log transform
prices = np.append(prices,prediction)
return prediction, prices
prediction, prices = inverse_predict(X[-1],max,min) #X[-1] is the last 60 days price
And here is a quick visual chart depicting the past data and the predicted price.
import matplotlib.pyplot as plt
plt.figure(figsize=(10,6))
plt.plot(range(61), prices, linestyle='-', marker='o', color='red', label='Predicted Data')
plt.plot(range(60), prices[:60], linestyle='-', marker='o', color='blue', label='Actual Data')
plt.title(f"{ticker} Stock Price: Last 60 Days and Next Day Predicted")
plt.xlabel('Date')
plt.ylabel('Price')
plt.legend()
plt.savefig(f"{ticker}_stock_price.png")