theoretical statistics

I. Probability Review

Laws of Probability Theory

(1) De Morgans Laws:
$$(A \cup B \cup C)^c = A^c \cap B^c \cap C^c$$ (2) Law of Total Probability:
- prob of event A occuring is equal to sum of event A occurring in all possible scenarios $$P(A) = P(A|B)P(B) + P(A|B^c)P(B^c)$$ (3) Inclusion-Exclusion Principle:
$$P(A \cup B) = P(A) + P(B) - P(A \cap B)$$ Conditional Probability:
$$P(A|B) = \frac{P(A \cap B)}{P(B)}$$ $$P(A \cap B) = P(A|B)P(B) = {}^* P(B|A)P(A) $$ * Bayes Theorem!
(1) Marginal Independence:
- A and B are marginally independent if:
$$P(A|B) = P(A)$$ $$P(A \cap B) = P(A)P(B)$$ (2) Conditional Independence:
- A1 and A2 are conditionally independent given B if: $$P(A_1 \cap A_2 | B) = P(A_1|B)P(A_2|B)$$

Random Variables & Distributions

CDFs and PDFs:
- By FTC, the PDF is equal to the derivative of the CDF
- Integrating the PDF from -∞ to x gives us the CDF $$F_X(x) = P(X \leq x) = \int_{-\infty}^{x} f(t) \, dt$$ $$f_X(x) = \frac{d}{dx} F(x)$$ Expectation:
$$\mathbb{E}[X] = \sum_{i} x_i P(X = x_i) \quad \text{(for discrete variables)}$$ $$\mathbb{E}[X] = \int_{-\infty}^{\infty} x f_X(x) \, dx \quad \text{(for continuous variables)}$$ (1) Linearity Rule: $$\mathbb{E}[aX + bY] = a\mathbb{E}[X] + b\mathbb{E}[Y]$$ (2) Sum Rule: $$\mathbb{E}\left[\sum_{i=1}^{n} X_i\right] = \sum_{i=1}^{n} \mathbb{E}[X_i]$$ (3) Expectation of a Function:
\[ E[g(X)] = \sum_{x} g(x) P(X = x) \] \[ E[g(X)] = \int_{-\infty}^{\infty} g(x) f_X(x) \,dx \] (4). Independence: \[ \text{If X and Y are independent} \rightarrow \quad E[XY] = E[X] \cdot E[Y] \] Variance:
$$\text{Var}(X) = \mathbb{E}[X^2] - (\mathbb{E}[X])^2$$ $$\text{Var}(cX) = c^2 \text{Var}(X)$$ $$\text{Var}(aX + bY) = a^2\text{Var}(X) + b^2\text{Var}(Y) + 2ab\text{Cov}(X,Y)$$

Joint Variables

- Marginal Densities tell us the probability of one variable by ignore the other (if given a joint dist. of weight and height, the marginal of weight tells us info on weight regardless of height)
- Conditional Densities tell us the probability of one variable given that you know the value of the other (if height is 5'6, whats prob that weight is 110?)

Discrete:
(1) Joint PMF: \[ P(X = x, Y = y) = p_{X,Y}(x,y) \] (2) Joint CDF: \[ F_{X,Y}(x,y) = P(X \leq x, Y \leq y) = \sum_{x' \leq x} \sum_{y' \leq y} p_{X,Y}(x', y') \] (3) Marginal PMFs can be obtained from the joint PMF: \[ p_X(x) = \sum_{y} p_{X,Y}(x,y) \] \[ p_Y(y) = \sum_{x} p_{X,Y}(x,y) \]
Continuous:
(1) Joint CDF is obtained by integrating the PDF: \[ F_{X,Y}(x,y) = P(X \leq x, Y \leq y) = \iint_{-\infty}^{(x,y)} f_{X,Y}(u,v) \,du\,dv \] (2) Marginals obtained by integrating over opposite variable: \[ f_X(x) = \int_{-\infty}^{\infty} f_{X,Y}(x,y) \,dy \] \[ f_Y(y) = \int_{-\infty}^{\infty} f_{X,Y}(x,y) \,dx \]
Covariance:
\[ \text{Cov}(X, Y) = E\left[(X - E[X])(Y - E[Y])\right] \] \[ \text{Cov}(X, Y) = E[XY] - E[X]E[Y] \] (1) Covariance of a Constant: \[ \text{Cov}(X, c) = 0 \] (2) Covariance of a Random Variable with Itself: \[ \text{Cov}(X, X) = \text{Var}(X) \] (3) Covariance of a Linear Combination: \[ \text{Cov}(aX + bY, Z) = a \, \text{Cov}(X, Z) + b \, \text{Cov}(Y, Z) \] (4) Correlation: \[ \text{Corr}(X, Y) = \frac{\text{Cov}(X, Y)}{\sigma_X \sigma_Y} \quad \sigma = \text{sd} \quad \sigma^2 = \text{var} \]

Moment Generating Functions (MGFs)

MGFs can help us find the distributions of SUMS of independent RVs.

(1) Zero'th moment is always = 1
(2) First moment is always = $ E(X) $
(3) Second moment is $ E(X^2) $ and can tell us the variance $ \sigma^2 = E(X^2) - [E(X)]^2 $
\[ M_X(t) = \mathbb{E}[e^{tX}] = \begin{cases} \sum e^{t x} p(x) \quad \text{(discrete)} \\ \\ \int_{}^{} e^{t x} f(x) \, dx \quad \text{(continuous)} \end{cases} \] (1) MGF of the sum of independent RVs is the product \[ M_{X_1 + X_2 + \cdots + X_n}(t) = M_{X_1}(t) M_{X_2}(t) \cdots M_{X_n}(t) \] because \[ \mathbb{E}[e^{t(X_1 + X_2)}] = \mathbb{E}[e^{tX_1}] \cdot \mathbb{E}[e^{tX_2}] \] (2) The k'th Derivative is the k'th Moment: \[\mathbb{E}[X^k] = M_X^{(k)}(0) \] (3) Continuity Theorem:
X_n and X are real-valued random variables: \[ X_n \xrightarrow{d} X \quad \text{as} \quad n \to \infty \quad (\text{convergence in distribution}) \] if and only if \[ M_{X_n}(t) \to M_X(t) \quad \text{as} \quad n \to \infty \quad \text{for all} \quad t. \]

Transformations of Random Variables

(1) We know some pdf $ f_X (x) $
(2) We know some function $ Y = g(X) $ (where g is continuous and strictly monotone)
(3) We want to find the pdf $ f_Y (y) $
(4) Find the inverse of $ Y = g(X) $, so solve for X
(5) Find the derivative of (4)
(6) Plug in $ f_Y (y) = f_X (4) * |5| $

Application: Generating iid RVs ~F from Uniform RVs!
(1) Lets say I want to generate X1, X2,... Xn iid from some general distribution function F (given F is continuous and strictly increasing)
(2) We can sample U1, U2... Un iid from Unif(0,1)
(3) Then generate Xi = F^-1(Ui)

Choose the distribution $ X $ you want to sample from (e.g., exponential, uniform, normal, etc.). Determine the CDF $ F_X(x) $ of the desired distribution. Set the uniform random variable $ U $ equal to the CDF: \[U = F_X(x)\] Rearrange the equation to solve for $ x $ in terms of $ U $: \[x = F_X^{-1}(U)\] Use a random number generator to obtain values of $ U $ and apply the above equation to generate samples from the desired distribution. Pretty damn cool if you ask me.

Central Limit Theorem (CLT) & Law of Large Numbers (LLN)

(1) CLT: The sum of a large number of i.i.d RV's tend to follow a normal distribution. AKA "convergence in distribution" to a normal.
\[\bar{X}_n = \frac{1}{n} \sum_{i=1}^{n} X_i \quad \quad Var(\bar{X}_n) = \frac{\sigma^2}{n} \] \[ \sqrt{n} ( \bar{X}_n - \mu) \quad \xrightarrow{d} \quad \mathcal{N}(0, \sigma^2) \quad \text{as } n \to \infty\] Rewriting this, we can say that \[ \bar{X}_n \thicksim N( \mu, \frac{\sigma^2}{n} ) \quad \text{or} \quad \bar{X}_n \thicksim \mu + \frac{\sigma}{\sqrt{n}} Z \] (2) LLN: As sample size n increases, sample mean converges to expected value. AKA "convergence to probability", the deviation of X from its mean tends to zero as n goes to infinity.
\[\bar{X}_n \xrightarrow{p} \mu \quad \text{as } n \to \infty\] \[\mathbb{P}(|\bar{X}_n - \mu| \geq \epsilon) \to 0 \quad \text{for any } \epsilon > 0 \text{ as } n \to \infty\]

Sample Moments Using LLN
- If $ X_i $ are iid and $ Var(X_i^k) < \infty $, sample moments are consistent estimators of the population k'th moment \[ \frac{1}{n} \sum_{i=1}^{n} X_i^k \quad \xrightarrow{p} \quad \mathbb{E}[X^k] \quad \text{as} \quad n \to \infty \]

Markov's Inequality:
- Markov tells us that probability of X >= a can never exceed the mean of X divided by a
- Suppose a = 100 * E(X), then P(|X| > 100 E(X) ) <= 1 / 100 (so the probability that X is 100 times greater than its mean must not exceed 1 / 100 \[ \mathbb{P}(|X| \geq a) \leq \frac{\mathbb{E}[X]}{a} \quad \text{for } a > 0 \] Chebyshev's Inequality:
- Quantifies how much the spread of a distribution can vary
- Suppose k = 4, then the right side is 1/16. The probability that X lands 4 times away from its SD is less than 1/16. \[ \mathbb{P}(|X - E[X]| \geq k) \leq \frac{Var(X)}{k^2} \quad \text{for } k > 0 \] \[ \mathbb{P}(|X - \mu| \geq k\sigma) \leq \frac{1}{k^2} \quad \text{for } k > 0 \]

Proof of Weak Law of Large Numbers using Chebyshev's Inequality
Show that sample mean $ \bar{X}_n $ converges in probability to $ \mu $ as $ n \to \infty $, i.e., \[ \forall \epsilon > 0, \lim_{n \to \infty} \mathbb{P}(|\bar{X}_n - \mu| \geq \epsilon) = 0 \] Apply this to the sample mean $ \bar{X}_n $. Since $ \mathbb{E}[\bar{X}_n] = \mu $ and $ \text{Var}(\bar{X}_n) = \frac{\sigma^2}{n} $, we have: \[ \mathbb{P}(|\bar{X}_n - \mu| \geq \epsilon) \leq \frac{\text{Var}(\bar{X}_n)}{\epsilon^2} = \frac{\sigma^2}{n \epsilon^2} \] As $ n \to \infty $, the right-hand side $ \frac{\sigma^2}{n \epsilon^2} $ tends to 0. Therefore, \[ \lim_{n \to \infty} \mathbb{P}(|\bar{X}_n - \mu| \geq \epsilon) = 0 \]

Convergence Theorems

- Besides using
(1) LLN for $ \xrightarrow{p} $
(2) CLT for $ \xrightarrow{d} $

1. Continuous Mapping Theorem (CMT)
The CMT allows us to apply FIXED continuous functions to converging sequences of random variables.
If $X_n \xrightarrow{p} X$, and $g(\cdot)$ is a fixed continuous function, then: \[ g(X_n) \xrightarrow{p} g(X) \]

2. Delta Method
If $X_n$ is a sequence of random variables and $g(\cdot)$ is differentiable: \[\sqrt{n}(X_n - \theta) \xrightarrow{d} N(0, \sigma^2)\] \[\sqrt{n}(g(X_n) - g(\theta)) \xrightarrow{d} N(0, \sigma^2 [g'(\theta)]^2)\]
Or we can also say that if $ \mathbb{E}[X_n] = \mu $ and $ Var(X_n) $ is small, then: \[ \mathbb{E}[f(X_n)] = f(\mu) \] \[ Var(f(X_n)) = \sigma^2(f'(\mu))^2 \]

3. Slutsky's Theorem
If there is convergence in BOTH distribution and probability (to a constant): Let $X_n \xrightarrow{d} X$ and $Y_n \xrightarrow{p} c$. Then: \[ \text{(1)} \quad X_n + Y_n \xrightarrow{d} X + c\] \[\text{(2)} \quad X_n Y_n \xrightarrow{d} cX\] \[\text{(3)} \quad \frac{X_n}{Y_n} \xrightarrow{d} \frac{X}{c}\]

II. Statistics of Sampling

Confidence Interval

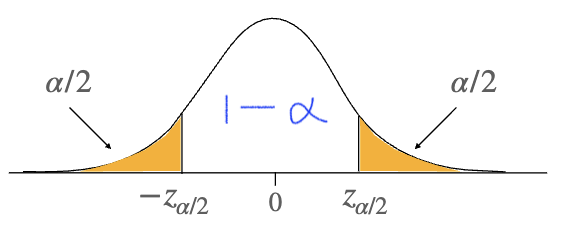
\[\mathbb{P}\left(-z_{\frac{\alpha}{2}} \leq \frac{\bar{X} - \mu}{\sigma_{\bar{X}}} \leq z_{\frac{\alpha}{2}}\right) = 1 - \alpha\] \[\mathbb{P}\left( \bar{X} - z_{\frac{\alpha}{2}}\sigma_{\bar{X}} \leq \mu \leq \bar{X} + z_{\frac{\alpha}{2}}\sigma_{\bar{X}} \right) = 1 - \alpha\]
When $ \sigma $ is KNOWN, we have $ \sigma_{\bar{X}} = \frac{\sigma}{\sqrt{n}} $.
But if $ \sigma $ us UNKNOWN , we can obtain an estimator: \[ \hat{\sigma}^2 = \frac{1}{n} \sum_{i=1}^{n} (X_i - \bar{X})^2 \quad \quad \text{(sample variance)} \]
Sample Variance
- Sample variance $ \hat{\sigma}^2 $ is biased estimator of population variance $ \sigma^2 $.
- Intuitively, we know that $ X_i $ is closer to $ \bar{X} $ than the true mean so variance is lower, so the below formulas make sense \[ \mathbb{E}[\hat{\sigma}^2] = \frac{n-1}{n} \sigma^2 \] To obtain an unbiased estimator, we adjust by multiplying the inverse so we can get: \[ S^2 = \frac{n}{n-1} \hat{\sigma}^2 = \frac{1}{n-1} \sum_{i=1}^{n} (X_i - \bar{X})^2 \] \[ \mathbb{E}[\hat{\sigma}^2] = \sigma^2 \] * note that these are for sampling with replacement (WR).
Use Finite Population Correction for sampling WITHOUT replacement
\[(1 - \frac{n-1}{N-1})\]

Differences between SD and SE \[ SE(\bar{X}) = \frac{S}{\sqrt{n}} = \frac{\sigma}{\sqrt{n}} \] \[ SD(\bar{X}) = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (X_i - \bar{X})^2} \]

Chi-Squared $ \chi^2 $ and $ t$

(1) Chi-Squared
- The Chi Squared distribution is represented by the sum of independent squared Normal random variables with n degrees of freedom: \[X \sim \chi^2_n \quad \text{where} \quad X = Z_1^2 + Z_2^2 + \dotsc Z_n^2 \quad \text{and} \quad Z \sim N(0,1)\] and actually \[\chi^2_n \sim \text{Gamma}(\frac{n}{2} , \frac{1}{2}) \] CLT tells us \[\chi^2_n \sim N(n, 2n) \] * Note if $ U \sim \chi^2_{n} $ and $ V \sim \chi^2_{m} $, and U and V are independent, then $ U + V \sim \chi^2_{n + m} $

(2) t-Distribution
The t-distribution is useful for making inferences based on small sample sizes. If Z and X are independent: \[ t = \frac{Z}{\sqrt{\frac{X}{n}}}, \quad Z \sim N(0,1), \quad X \sim \chi^2_n \] * $ t_n \xrightarrow{d} Z \sim N(0,1) $ as n goes to infinity.
* t has a fatter tail distribution than Z, and as the n degrees of freedom increases, it slims and looks more like a Normal

Interested in the quantity \[ \frac{\bar{X} - \mu}{SE(\bar{X})} \sim t_{n-1} = \]

Stats from Normal Population

Multivariate Normal

A random vector $ \mathbf{X} $ follows a multivariate normal distribution if: (A is p x q) \[ \mathbf{X} = AZ + \mu \quad \sim \quad \mathcal{N}_p(\mathbf{\mu}, \Sigma) \quad \quad (\Sigma = A A^T) \] \[ \text{where} \quad \quad Z \sim N_q(0, I) \quad \quad \text{is a spherical normal} \] (1) $ \mathbb{E}[X] = A*E[Z] + \mu = \mu \in \mathbb{R}^p $
(2) $ \text{Var}(X) = \text{Cov}(X) = \Sigma \in \mathbb{R}^{p \times p} $ where $ \Sigma_{i,j} = \text{Cov}(X_i, X_j) $.

Method of Moments

Goal: We have some data. We understand the properties of some known distributions. Let us describe the data as generated from some natural distribution. One way to describe distributions can be through its moments. For instance:
- the first moment (mean) tells the central location
- the second moment shows the spread
- higher moments like skew and kurtosis describe the shape

Typically, the number of parameters we want to estimate = the number of moments we can find. We can express as a function of the moments: \[ \mu_k = \mathbb{E}[X^{(k)})] \] Suppose we want to estimate two parameters: The general form is \[ \theta_1 = f_1(\mu_1, \mu_2) \] \[ \theta_2 = f_2(\mu_1, \mu_2) \] but we want to estimate it using sample moments (bc we usually dont have access to the whole population) \[ \hat{\mu_k} = \frac{1}{n} \sum{X^{(k)}_i} \] \[ \hat{\theta_1} = f_1(\hat{\mu_1}, \hat{\mu_2}) \] \[ \hat{\theta_2} = f_2(\hat{\mu_1}, \hat{\mu_2}) \]

Sampling Distributions of MOMs

Goal: We want to see how stable our estimated parameters are. To do so, we analyze it's sampling distributions (mean, variance, SE) so we can also construct confidence intervals. There are two ways we can see the sampling distributions of these parameter estimates: bootstrap sampling and large sample approximations

(1) By bootstrap simulation, we can estimate standard error as the following
- Sample n datapoints like 1000 times
- Each iteration from 1 to 1000 provides us with an estimate of parameter p* \[ SE_{\hat{p}} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (p^*_i - \bar{p})^2} \]
(2) Large sampling approximation is based on consistency (LLN): as the number of $ \hat{\theta} $ increase, the estimators become more correct to a true estimates, as well as asymptotic normality (CLT).
- See delta method

Cumulant Generating Functions and Kurtosis/Skew
Let $ K(t) = log(M_X(t)) $ be the cumulant generating function of X and $ k_n = K^{(n)}(0) $ \[ \text{Skew}(X) = \frac{k_3}{k^{3/2}_2} = \frac{\mathbb{E}[(X - \mu)^3]}{\sigma^3} \] \[ \text{Kurt}(X) = 3 + \frac{k_4}{k^{2}_2} = \frac{\mathbb{E}[(X - \mu)^4]}{\sigma^4} \]

Maximum Likelihood

Say we have datapoints $X_1 \ldots X_n $ with a joint density function $ f(x_1 \ldots x_n | \theta) $. Our goal is to find the parameters $ \theta $ so that we maximize the probability of observing these datapoints $ X_i $.

If they are assumed to be iid, then the likelihood function is considered as a product of the individual densities of X given $ \theta $. But its easier to take the log likelihood since multiplying a bunch of probabilities < 1 will go to zero \[ l(\theta) = \sum{logf(X_i | \theta)} \] To find the $ \theta $ that maximizes the log likelihood function, we take its first derivative (or partial derivations) and set = 0 and solve for $\theta $. \[ \text{score function} \quad l'(\theta) = 0 \] Local/Global Max: We can also (further) ensure that the root is at least a local max by checking $ l''(\hat{\theta}) < 0 $, or global for ex if the function is also concave.

Likelihood Ratio
- How much more probable it is that our estimated parameter is = to x than opposed to some other value y.

\[ \frac{l(\hat{\theta} = x)}{l(\hat{\theta} = y)} \] Sampling distribution of MLE
- We can follow a similar approach as MOM (either bootstrapping or large sample approx)
- The SE of MLE is generally smaller and more optimal compared to other estimators like MOMs
- Under regularity conditions (where the bounds is NOT dependent on $ \theta $ -- so Unif(0,$\theta$) would be invalid) then: \[ \mathbb{E}[l'(\theta)] = 0 \] \[ \mathbb{E}[-l''(\theta)] = I(\theta) \] Fisher Information $ I(\theta) $
- The amount of information that our data can provide about our true parameter
- For n iid RVs, the Fisher Info of the total sample is $ I_{n}(\theta) = n I(\theta)$
- Inversely proportional to variance under asymptotic normality and regularity conditions $ Var(\hat{\theta}) = \frac{1}{I(\theta)} $
\[ I(\theta) = \mathbb{E}[-l''(\theta)] \]

(1) Consistency of MLE (LLN)

If $X_1 \ldots X_n$ are iid with a true value of $\theta$
\[ \hat{\theta}_{MLE}(X_1 \ldots X_n) \xrightarrow{p} \theta \] We can also show the relationship between the KL divergence and Fisher Information for small $\hat{\theta} - \theta $ \[ D_{\text{KL}}(\theta,\hat{\theta}) = \frac{1}{2} (\hat{\theta} - \theta)^2 I(\hat{\theta}) \]

(2) Asymptotic Normality of MLE (CLT)

*MLE is asymptotically efficient because the asymptotic variance is equal to bound given by Cramer Roa \[ \sqrt{n}(\hat{\theta} - \theta) \xrightarrow{d} N\left(0, \frac{1}{I(\theta)} \right) \]

Confidence Intervals for MLE

The distribution of $ \sqrt{nI(\theta)}(\hat{\theta} - \theta) $ is approximately Standard Normal $ \sim N(0,1) $
\[ P(-z_{a/2} \leq \sqrt{nI(\theta)}(\hat{\theta} - \theta) \leq z_{a/2} ) = 1 - a \] \[ \hat{\theta} \pm z_{a/2} \frac{1}{\sqrt{nI(\hat{\theta})}} \]

Comparing Estimators

We can assess which estimator (i.e., MOM vs MLE estimators) is better using the Mean Squared Error:
\[ MSE(\hat{\theta}) = \mathbb{E}[(\hat{\theta}(X) - \theta)^2] = \int (\hat{\theta}(X) - \theta)^2 f(x|\theta) dx\] Variance-Bias Decomposition
\[ MSE(\hat{\theta}) = \mathbb{E}[(\hat{\theta}(X) - \theta)^2] = Var(\hat{\theta}) + [\mathbb{E}\hat{\theta} - \theta]^2 \]

Efficiency & Cramer Roa Bound in MLE

Cramer-Roa Bound: the optimal (lowest possible) variance for some unbiased estimator. Functions as a benchmark against any estimator

Suppose $ \bar{X} \sim N(\theta, \sigma_{n}^2) $ and $ \hat{\theta}_{a} = a\bar{X} $. We have $ Var(\hat{\theta}_{a}) = a^2 \sigma_{n}^2 $:
- a = 1 unbiased, all variance
- a = 0, all bias, no variance
\[ MSE(\hat{\theta}_{a}, \theta) = a^2 \sigma_{n}^2 + (1 - a)^2 \theta^2 \]
If $ \hat{\theta} $ is unbiased: $ E\hat{\theta} = \theta $, then $ MSE(\hat{\theta}_{a}, \theta) = Var(\hat{\theta}) $. So to compare two unbiased estimators, we just focus on comparing their variances.
\[ eff(\hat{\theta}_{1}, \hat{\theta}_{2}) = \frac{Var(\hat{\theta}_{1})}{Var(\hat{\theta}_{2})} \]
Def: Cramer Roa Bound (CRB)
If $ \hat{\theta} $ is an unbiased estimator of $ \theta $, then the minimum possible variance of that estimator is shown below. If it achieves this, the estimator is said to be efficient (for some fixed n) \[ Var(\hat{\theta}) \geq \frac{1}{nI(\theta)} \] Folk Theorem:
- Shows MLE is asymptotically efficient
Combining asymptotic normality and CRB, it follows that if a sequence of estimators such as $ T_n $ is consistent and asy. normal, then: \[ \sqrt{n}(T_n - \theta) \xrightarrow{d} N(0, Var(\theta)) \] \[ Var(\theta) \geq \frac{1}{I(\theta)} \] And the approx CI is wider than the MLE interval, (showing MLE is optimal): \[ T_n \pm z_{a/2} \frac{Var(T_n)}{\sqrt{n}} \]

Hypothesis Testing

Likelihood Function
Tells us the probability of a null hypothesis compared to an alternative hypothesis. \[ \frac{f(x | H_0)}{f(x | H_a)} \]
Type I Error (False Positive): Null is true but we accept alt
- Probability of Type I error denoted by $ \alpha $
- Choose some $ C $ to control $ \alpha $ (where C is some threshold value to accept the null) \[ P_{\mu = 0} (\bar{X} > C) = P(Z > C\sqrt{n}) = 1 - \Phi(C\sqrt{n}) = \alpha \]
Type II Error (False Negative): Alt is true but we accept null
- Probability of Type II error denoted by $ \beta $
- Power (True Negative) = $ 1 - \beta $ \[ P(Z > z_{\alpha} - \mu_1 \sqrt{n}) = 1 - \Phi(z_{\alpha} - \mu_1 \sqrt{n}) = 1 - \beta \] \[ \beta = \Phi(z_{\alpha} - \mu_1 \sqrt{n}) = \Phi(-z_{\beta}) \]

Discreteness
In discrete cases, you can’t always hit your exact $ \alpha $. A theoretical fix is to add some randomness (like flipping another coin) to reach the exact level

Neyman-Pearson Lemma:
Justifies likelihood ratio as the optimal way to maximize power (reduce false negatives) and control false positives (for simple tests with single probability distributions)
- Usually used for simple tests (where all parameters are specified and known) - Can be extended to find the uniformly most powerful: if there are many possible values of the parameter, then these tests will be most powerful for every possible value of that parameter but only for one sided tests not two
- One-Sided: Tests if something is greater or less than a certain value
- Two-Sided: Tests if something is different from a certain value

p-value
Smallest significance value at which null would be rejected
The confidence interval contains all those values for which the null hypothesis is accepted.

Generalized Likelihood Ratio
\[ \log \Lambda = \max_{\theta \in \omega_0} \ell(\theta) - \max_{\theta \in (\omega_0 \cup \omega_1)} \ell(\theta) \]